Снежинки, которых мы не знаем

В 1635 году формой снежинок заинтересовался французский философ, математик и естествоиспытатель Рене Декарт, написавший трактат «Опыт о метеорах». Декарт впервые нашел и описал достаточно редкую двенадцатиконечную снежинку. До сих пор неясно, при каких условиях она образуется.

В 1665 году Роберт Гук увидел с помощью микроскопа и опубликовал множество рисунков снежинок самой разной формы.

#Снежинки и их разновидности

В первой части фильма мы знакомимся с разнообразием.

#Секреты образования снежинок

Во второй части фильма раскрываются секреты возникновения фракталов - снежинок.

#Классификация типов снежинок

Известно несколько классификаций снежных кристаллов. В 1951 году Комиссией снега и льда Международной ассоциации гидрологических наук предложена классификация, различающая семь основных форм кристаллов:

• пластинки,
• звездчатые кристаллы,
• столбцы или колонны,
• иглы,
• пространственные дендриты,
• столбцы с наконечниками
• неправильные формы.

И еще три вида твердых осадков: мелкая снежная крупка, ледяная крупка и град.

Существует и более развернутая классификация.

При падении снежных кристаллов с ними может случиться многое - частичное таяние, столкновения друг с другом и с каплями воды. Вот почему наиболее часто встречаются нерегулярные кристаллы, не имеющие легко идентифицируемой формы. Иногда кристаллы представляют собой комбинацию нескольких форм.

#Формы снежинок при различных температурах и влажности

С понижением температуры обычно снежинки становятся более мелкими. Меняется и форма снежинок: от красивых правильных звездочек - к пластинкам и неправильным столбикам.

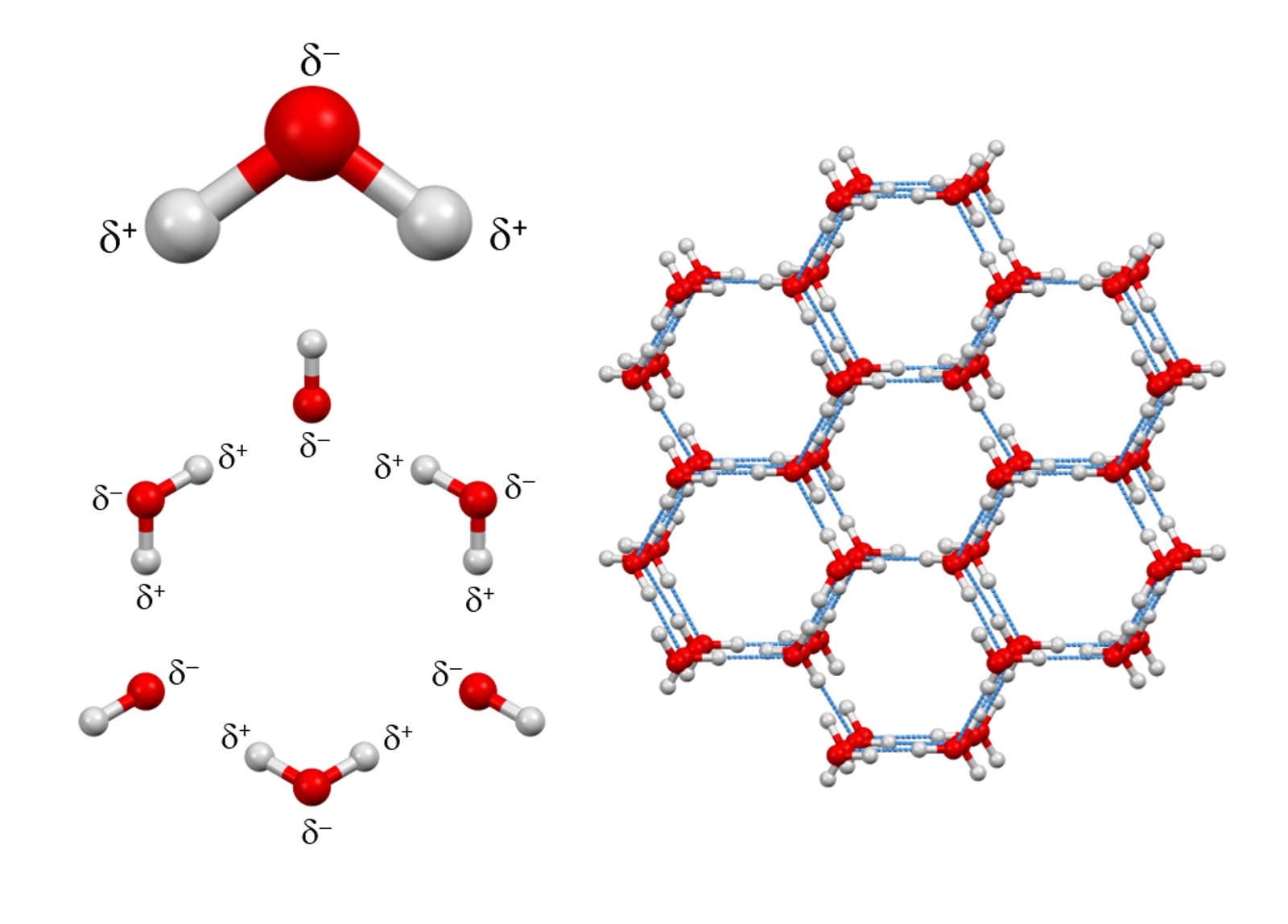
Молекулы воды в кристалле льда формируют шестиугольную решетку. На рисунке ниже красные шары – это атомы кислорода, между ними – атомы водорода. Шестикратная симметрия снежинок берет свое начало от кристаллической решетки льда - между лучами кристалла возможны углы лишь в 60° и 120°. Каждая молекула воды окружена четырьмя ближайшими к ней молекулами, находящимися на одинаковых расстояниях от нее и размещенных в вершинах правильного тетраэдра.